Algorithmic Optimization Solutions: Unleashing the Power of Algorithms for Enhanced Performance
In today’s digital landscape, where online visibility is crucial for success, businesses are constantly seeking ways to improve their online presence. Enter algorithmic optimization solutions – a game-changer in the realm of digital marketing and search engine optimization (SEO).
But what exactly are algorithmic optimization solutions? Simply put, they are advanced techniques that leverage the power of algorithms to enhance online performance. These solutions utilize data-driven insights and cutting-edge technologies to optimize websites, content, and marketing strategies.
One of the key benefits of algorithmic optimization solutions is their ability to adapt and evolve. Algorithms have the capacity to analyze vast amounts of data, identify patterns, and make intelligent decisions based on this information. This allows businesses to stay ahead of the competition by continuously refining their digital strategies.
One area where algorithmic optimization solutions excel is in SEO. Search engines like Google use complex algorithms to determine search rankings. By understanding these algorithms and tailoring strategies accordingly, businesses can significantly improve their organic search visibility.
These solutions encompass a wide range of techniques, including keyword analysis, on-page optimization, link building, content creation, and technical SEO. Algorithmic optimization solutions take into account factors such as user experience, relevance, authority, and website performance – all crucial elements in achieving higher search rankings.
Furthermore, algorithmic optimization solutions go beyond traditional SEO practices. They delve into data analysis to uncover valuable insights about user behavior and preferences. By understanding how users interact with websites and content, businesses can tailor their strategies to deliver a more personalized experience.
Algorithmic optimization also extends its reach to other areas of digital marketing. From social media advertising to pay-per-click campaigns, these solutions help optimize every aspect of a business’s online presence. By harnessing the power of algorithms in these areas too, businesses can maximize their return on investment (ROI) while reaching target audiences effectively.
The beauty of algorithmic optimization solutions lies in their ability to provide measurable results. With the help of advanced analytics tools, businesses can track key performance indicators, monitor progress, and make data-driven decisions. This ensures that strategies are continuously refined and improved for optimal outcomes.
In conclusion, algorithmic optimization solutions are revolutionizing the way businesses approach digital marketing and SEO. By harnessing the power of algorithms, businesses can unlock new levels of online performance and stay ahead in today’s competitive landscape. Whether it’s improving search rankings, enhancing user experience, or maximizing ROI, these solutions are a must-have for any business looking to thrive in the digital age. Embrace algorithmic optimization solutions and unleash the true potential of your online presence.
Frequently Asked Questions: Algorithmic Optimization Solutions
- What are algorithmic solutions?
- Which algorithm provides optimization solution?
- What is the best optimization algorithms?
- What is optimization techniques in algorithms?
What are algorithmic solutions?
Algorithmic solutions refer to techniques and strategies that utilize algorithms to solve complex problems or optimize processes. Algorithms are step-by-step procedures or sets of rules designed to perform specific tasks or calculations. In the context of algorithmic solutions, these algorithms are applied to various domains such as data analysis, optimization, artificial intelligence, and more.
Algorithmic solutions are used in a wide range of fields and industries. For example, in computer science, algorithms play a fundamental role in developing software applications, designing efficient data structures, and solving computational problems. In finance, algorithmic trading uses sophisticated algorithms to analyze market data and make automated trading decisions.
In the realm of optimization, algorithmic solutions aim to find the best possible solution for a given problem within a set of constraints. These solutions often involve mathematical models and optimization techniques that leverage algorithms to explore potential solutions and identify the most optimal outcome.
In data analysis and machine learning, algorithmic solutions are used to uncover patterns, insights, and predictions from large datasets. Algorithms enable the processing of vast amounts of data efficiently and help automate decision-making processes based on statistical analysis.
Additionally, algorithmic solutions can be employed in various other areas such as image recognition, natural language processing, recommendation systems, network routing optimization, logistics planning, scheduling problems, and more.
The power of algorithmic solutions lies in their ability to automate complex tasks or processes that would otherwise be time-consuming or error-prone if done manually. By leveraging algorithms effectively, businesses can streamline operations, improve efficiency, make informed decisions based on data-driven insights, and ultimately achieve better outcomes.
Overall, algorithmic solutions encompass a wide array of techniques that leverage algorithms to solve problems or optimize processes across different domains. They form the backbone of many technological advancements we see today and continue to drive innovation across industries.
Which algorithm provides optimization solution?
There are various algorithms that can be used to provide optimization solutions depending on the specific context and problem at hand. Some commonly used algorithms for optimization include:
- Genetic Algorithms: Inspired by the process of natural selection, genetic algorithms use a population-based approach to search for optimal solutions. They involve creating a set of potential solutions, applying genetic operators such as mutation and crossover, and iteratively improving the solutions over generations.
- Simulated Annealing: This algorithm is based on the annealing process in metallurgy. It starts with an initial solution and gradually explores the solution space by allowing “bad” moves initially but with decreasing probability over time. This stochastic search process helps escape local optima and find global or near-optimal solutions.
- Particle Swarm Optimization (PSO): PSO is inspired by the social behavior of bird flocking or fish schooling. It involves a population of particles that move through the solution space, adjusting their positions based on their own best-known position and the best-known position among all particles in the swarm.
- Ant Colony Optimization (ACO): ACO is inspired by the foraging behavior of ants. It simulates how ants deposit pheromone trails to mark paths and communicate with each other. By iteratively updating these trails based on solution quality, ACO can find good solutions for optimization problems such as routing or scheduling.
- Gradient Descent: Gradient descent is a widely used optimization algorithm for finding local minima or maxima of a differentiable function. It iteratively adjusts parameters in the direction of steepest descent (negative gradient) until convergence is achieved.
These are just a few examples of algorithms used for optimization purposes across various domains such as machine learning, operations research, and mathematical programming. The choice of algorithm depends on factors like problem complexity, available data, computational resources, and specific requirements of the optimization task at hand.
What is the best optimization algorithms?
The “best” optimization algorithm depends on the specific problem being addressed and the context in which it is applied. Different algorithms have different strengths and weaknesses, making them suitable for different scenarios. Here are a few popular optimization algorithms:
- Genetic Algorithms (GA): Inspired by natural selection and genetics, GA mimics the process of evolution to find optimal solutions. It utilizes techniques like crossover, mutation, and selection to iteratively improve solutions over generations.
- Particle Swarm Optimization (PSO): PSO is inspired by the social behavior of bird flocks or fish schools. It involves a population of particles that move through a search space, adjusting their positions based on their own best-known solution and the collective knowledge of the swarm.
- Simulated Annealing (SA): SA is based on the annealing process in metallurgy, where a material is heated and slowly cooled to reduce defects. SA uses a random search combined with probabilistic acceptance of worse solutions to explore the search space and escape local optima.
- Ant Colony Optimization (ACO): ACO is inspired by the foraging behavior of ants searching for food. It uses pheromone trails left by ants to guide other ants towards better solutions. ACO has been particularly successful in solving problems related to routing and scheduling.
- Gradient Descent: Gradient descent is an iterative optimization algorithm used in machine learning and deep learning models to minimize an objective function by adjusting model parameters in the direction of steepest descent.
- Tabu Search: Tabu Search maintains a short-term memory of previously visited solutions and uses this memory to avoid revisiting them during subsequent iterations, thus exploring new areas of the search space more effectively.
It’s important to note that no single algorithm can be considered universally “best.” The choice of algorithm depends on factors such as problem complexity, size of the search space, available computational resources, time constraints, and specific requirements of the problem at hand. It is often beneficial to experiment with multiple algorithms or use hybrid approaches to find the most suitable optimization solution for a given problem.
What is optimization techniques in algorithms?
Optimization techniques in algorithms refer to a set of methods and strategies used to improve the efficiency, performance, or quality of an algorithm. These techniques aim to find the most optimal solution or outcome within a given set of constraints.
There are various optimization techniques that can be applied to algorithms, depending on the specific problem or objective at hand. Some commonly used optimization techniques include:
- Greedy Algorithms: Greedy algorithms make locally optimal choices at each step with the hope that these choices will lead to a globally optimal solution. This technique is often used when finding an exact optimal solution is computationally expensive or impractical.
- Dynamic Programming: Dynamic programming breaks down complex problems into smaller overlapping subproblems and solves them in a bottom-up manner. It stores the solutions to these subproblems in a table, which can be referred to later when solving larger subproblems.
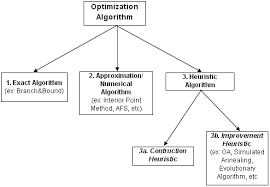
- Heuristic Algorithms: Heuristic algorithms are approximation algorithms that provide near-optimal solutions by making educated guesses or applying rules of thumb. They trade off optimality for efficiency and are commonly used when finding an exact optimal solution is not feasible within reasonable time constraints.
- Genetic Algorithms: Genetic algorithms mimic the process of natural selection and evolution to solve optimization problems. They use concepts such as mutation, crossover, and selection to iteratively generate new candidate solutions and improve upon them over generations.
- Simulated Annealing: Simulated annealing is inspired by the annealing process in metallurgy. It is a probabilistic technique that allows for occasional “bad” moves early on but gradually reduces these moves as the algorithm progresses towards an optimal solution.
- Linear Programming: Linear programming is a mathematical technique used to optimize linear objective functions subject to linear constraints. It involves formulating the problem as a system of linear equations and inequalities and finding the best feasible solution using optimization methods.
These are just some examples of optimization techniques commonly utilized in algorithm design and analysis. The choice of technique depends on the specific problem, the available resources, and the desired trade-offs between optimality, efficiency, and computational complexity.